Logistic Regression

前两篇文章中的模型Perceptron Learning Algorithm和Linear Regression可以解决的问题是判断一个患者是否会心脏病，但是实际生活中里面里面可能给出的报告的是患者患心脏病的一个概率：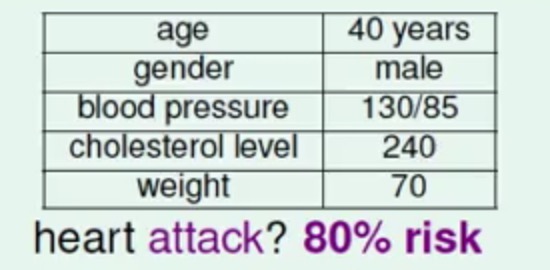

这样的话从模型的角度来说更希望的是得到一个发生在患心脏病的概率f(x)=P(+1|x)∈[0,1],
这个概率值越大，患心脏病的概率越大，反之则越小

这个也叫Soft Binary Classification，因为这里的概率可以根据一个阈值来判断是否属于哪一类

刚刚可以看到目标函数f(x)的值是属于一个[0,1]范围的值，理所应当，我们理想的训练数据应该是这样的

想法虽好，然是实际上训练目标的概率值很难得到（比如一个患者你过了两三个月之后也许可以观察到该用户是否会患上心脏病，但是你可能是无法知道他患心脏病的真实概率的）
所以我们拿到的真实数据是这样的

这样也可以你可以看成为上上概率训练数据一个有噪声的版本，每个标签值对应的0或者1都是直接在概率阈值上进行了一个分类了

那么现在的目标就是在原来（二分类）的数据上，以[0,1]范围为目标找到一个好的假设(hypothesis)

那么首先可以想到的是按Linear Regression一样在特征值和权重向量上进行一个加权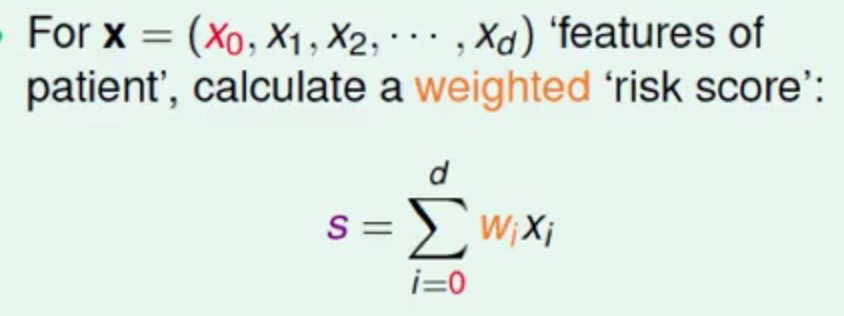

得到加权之后的score之后，我们希望score越高，最终得到的概率值越大（但是不能大于1），score越低，最终的概率值越小（不能小于0），那正好可以通过下面的函数的转换来完成刚刚的需求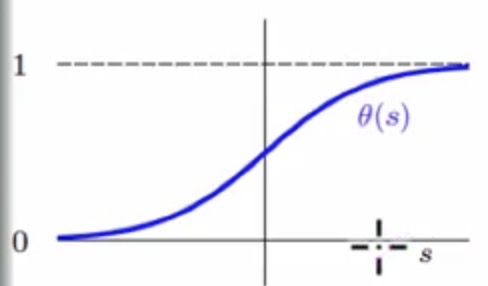

这个函数也叫做logistic function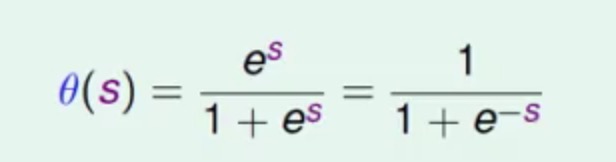

其中里面的s就是相当于score

最终我们可以得到的模型函数为

这也就是Logistic Regression的表示

Cross-Entropy Error

根据Logistic Regression的目标函数f(x)可以很容易得到如下关系

假如现在有如下的数据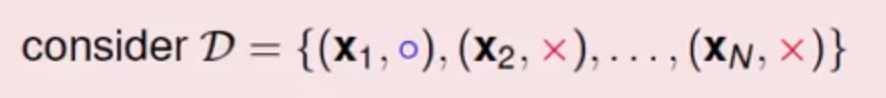

那么这批数据产生的概率是

使用f(x)替换可以得到

现在以hypothesis的角度来看，通过h(x)产生的样本情况为

如果h(x)≈f(x),那么我们就可以说通过h(x)产生的样本的可能性与真正f(x)产生的数据很接近
那么我们现在找

这个是建立在f(x)产生的数据的可能性很大的基础上，所以现在也相应的就是求h(x)产生的样本的可能性也要很大。
用式子表达出来就是这个

又因为logistic function的写对称性（1-h(x)=h(-x)），上面的式子可以转为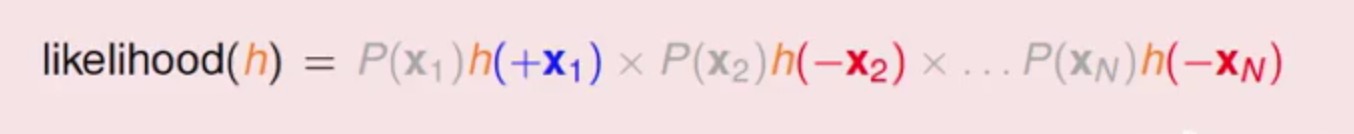

上面带负号的正好可以看做负样本(yn=-1)，带正好的也正好可以看做正样本(yn=+1)，同时对于每个hypothesis来说上图中灰色部分(产生各个数据的概率,不含目标)都是一样的，所以现在可以将上述式子简写为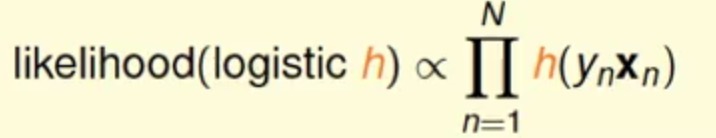

它是一个正比函数，yn正好可以替换为原来的正负1

现在要做的就是找到合适的h(x)，使的上述的可能性最高
把h用气w来替换为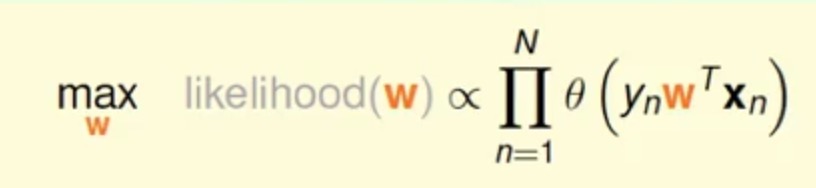

为了求其最优化，我们将上述式子的连乘转为连加，通过添加一个ln函数(单调递增)，同时使用添加负号来由求最大化转为最小化(方便求)
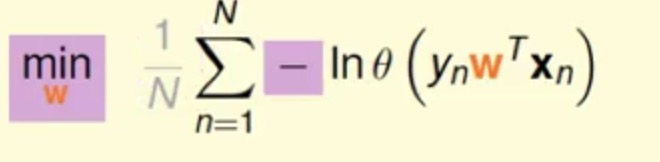（式子2）
这里继续使用logistic function函数进行替换，可以有

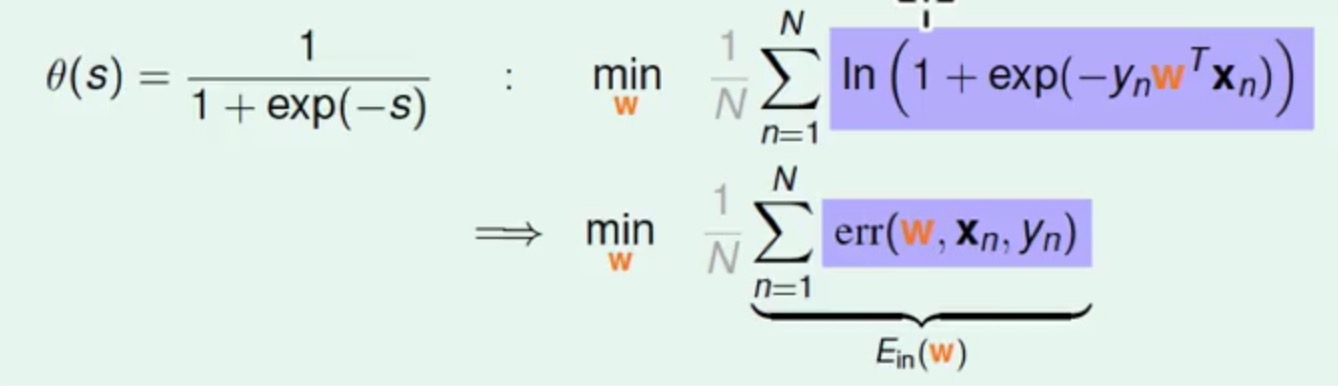
(替换技巧ln a/b=ln a- ln b和ln 1=0)
紫色背景的表示对x_n，y_n的Error，通过累加再求平均就是很熟悉的Ein了,这个Error就叫做Cross-Entropy Error

Gradient Descent

求式子2中的最小值最直观的就是对其求梯度并且其梯度在0的地方就是最小(也是最优)

这里能用上述的方法来求是因为Logistic Regression的Ein是可导可微的，并且是凸的

现在将其对w求偏导

上面求的是梯度里面的一个Component，那么对所有的Component都整理起来可以得到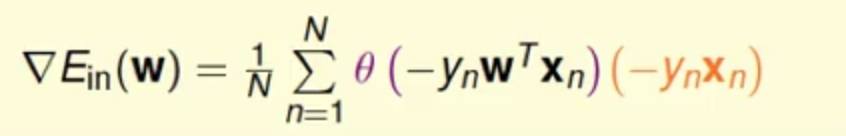

目标就变成了求上述梯度为0的情况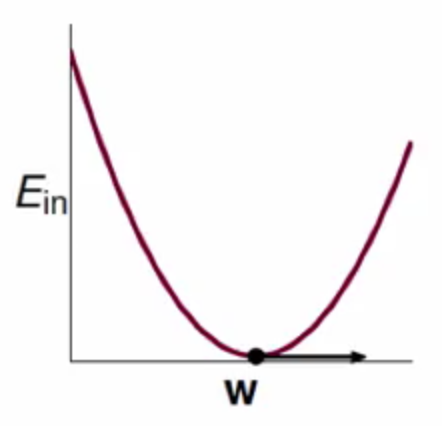

但是可以看到上述的梯度并不是一个一次的方程式，也就是无法直接求出具体的值(不能像Linear Regression中那样直接求出)

不过现在根据需要求解的问题看成现在这样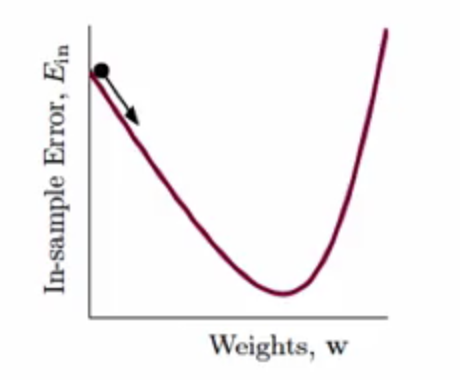

梯度的函数可以看成图种的曲线，而相应的参数w可以看成图种的那个球，每次都朝着错误的方向v滚，将球从上面滚到最低处，也就是得到梯度为0的情况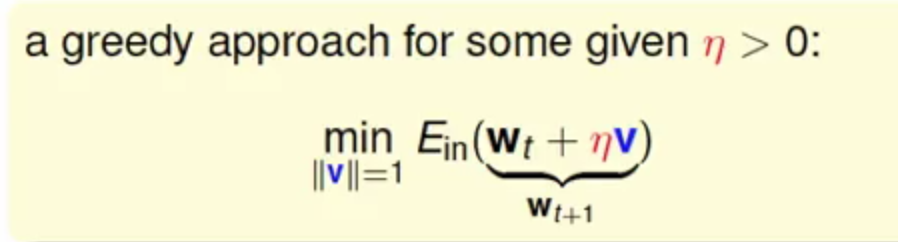

其中v为球滚动的方向（后面可以知道是梯度的反方向），还有η表示步伐的长度(为正数，越大会滚的越快)
现在的问题就是转为了如果很快滚下去，并且是走对方向（真实中并不是一个二维空间，往往是一个多维空间）

在曲线上很小很小的一个区间内可以看作是一个线段，那这样就可以在曲线上的一个点出来，然后走出一小段的线段来，那这样可以通过多维度的泰勒展开可以得到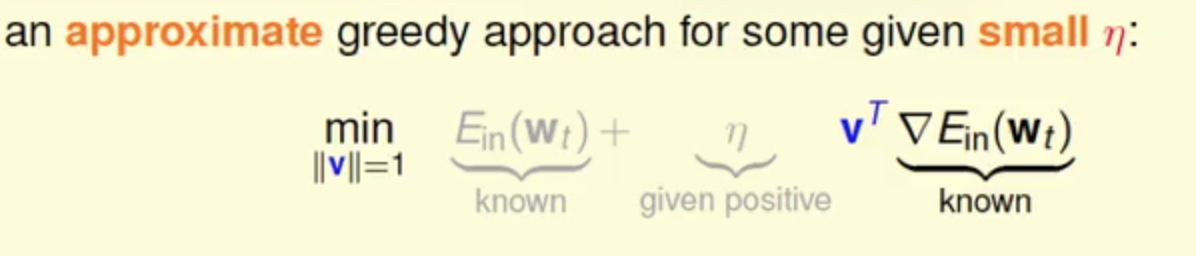

这里的η很小的时候，这个线段的逼近 还是很不错的

上面公式中的灰色标志是表示与v没什么关系，在求解最小化的过程中有颜色部分两个向量内积的最小，那这样的话两个向量完全反方向就是最小的，也就是说v走的是梯度反方向，并且需要注意的是他是单位向量，所以这里就会有

那么参数更新的方式就会有

这个就是梯度下降法(Gradient Descent)，也是一种较为简单的，有效的优化方法

好，到了这里v可以求了，那么η这个需要给定的参数取多少合适呢？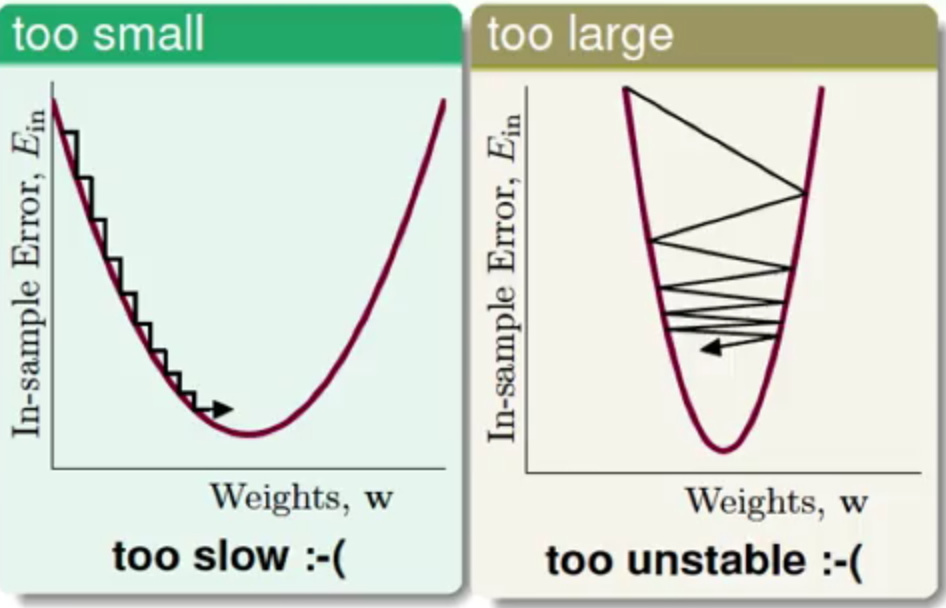

从上图中可以发现：

1. η很小：那么整个参数更新过程就会很慢，不过准确性（与最小值的接近程度）应该还是可以保证的
2. η很大，那么这个参数过程就会很不稳定，那么他的最终的准确性可能就会较低

比较推荐的是采用一种自适应的方法来做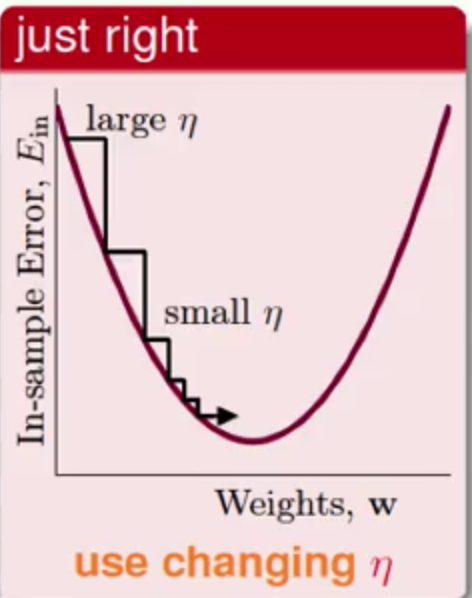

当梯度较大的时候，η也跨的较大，那么当梯度慢慢减小的时候，η也同时慢慢减少，也就是说η与梯度值会呈正相关的关系，那么这样在保证了准确性的同时，又可以加快速度^_^
此时根据η正比于梯度值的特性可以惊奇的发现

（图种红色的η为原生值，紫色的η为正比的比率）
在整个参数的更新过程中可以将梯度值的计算消除掉，这里的紫色的η也称为学习速率

现在Logistic Regression使用Gradient Descent来计算的过程为

1. 首先将w初始化为0向量
2. 不断迭代的遍历样本
3. 每遍历一次样本时都计算当前样本的梯度(可以发现每个样本的梯度都需要遍历整个样本之后才能计算得到-_-)
4. 计算完梯度之后往梯度的反方向更新权值w
5. 不断进行2~4的步骤，直到Ein足够小或者迭代次数足够多
6. 返回最后一个更新的w就作为我们的最优hypothesis

推导了这么久，但是最终发现整个计算过程还是比较简单清晰地，而且还有点像PLA的Pocket Algorithm

Stochastic Gradient Descent

现在这里再重新理解一下Gradient Descent算法：每次迭代在计算其中一个样本的梯度的时候，都需要遍历所有的样本对梯度的贡献进行求和，然后取平均值作为最后的梯度，是不是感觉代价偏大(牵一发而动全身的感觉-_-，特别是在现在大数据的情况下，这效率应该会很慢)
现在我们是希望求得这个梯度的方向，但是不希望通过遍历所有样本求和求平均来得到梯度，有一个巧妙的方法就是将这个过程看过一个随机过程的平均，随便去抽一个样本然后将其作为梯度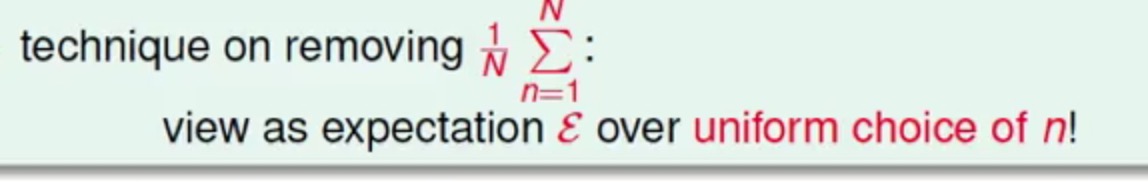

这种方式我们将随机的一个样本偏微分算出来的梯度称为随机梯度(Stochastic Gradient)，最终真实地梯度与这种随机方式求出来的梯度的期望是一致的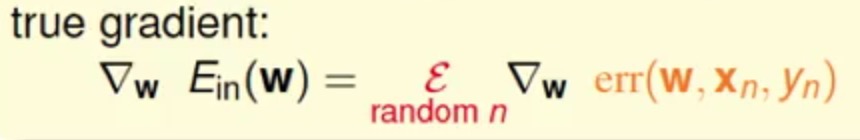

上面的过程就好比：现在有10000个数字，需要求这些数字的平均数，最普通的方法就是10000求和再求平均，但是遍历10000次的复杂度认为太大，另一种解决方法就随机抽一小批数据(比如100)再求和求平均，其实这两个期望是很类似的，现在另一种trick的方法是直接只抽一个数字，把它认为就是这10000个数字的平均数，现在再想想抽数字抽好多次最后结果喝第一次求和的期望也是类似的

这个方式可以认为：随机得梯度=真实梯度+一些噪声

这样的话在更新参数这一块的代价较大的梯度计算即可直接替换为轻量级的随机梯度，在足够多次的迭代之后，这个真实梯度的平均也会约等于随机梯度的平均
那么最终Stochastic Gradient Descent(SGD)算法的表示为

在整个算法计算过程中除了随机梯度计算的区别，还有其终止条件就是足够多的迭代，但是取的是Ein最小的那组作为最优

貌似林老师爆出来关于η参数的取值最优是0.1126 经验参数值哦^_^

SGD优势有:

1. 轻量级计算
2. 适合于大数据（因为复杂度低，计算梯度是O(1)）
3. 还可以进行online learning
4. 。。。其实我想说比较容易实现并行

劣势：就是可能不稳定

总结

Logistic Regression(LR)是一个线性的二分类模型，主要有以下优缺点
优点：

1. 实现简单；
2. 分类时计算量非常小，速度很快，存储资源低，也很容易并行；(在大量数据情况下这个模型非常适用，这也是好多广告系统首选的原因)
3. 在处理分类问题的同时还可能给出一个概率值(这个值有时候蛮有用的)
4. 优化方法多：除了GD和SGD，应该还有拟牛顿法、BFGS、L-BFGS

缺点：

1. 容易欠拟合，一般准确度不太高
2. 只能处理两分类问题（在此基础上衍生出来的softmax可以用于多分类），且必须线性可分；

参考

• 《台湾国立大学-机器学习基石》第十讲
• 《台湾国立大学-机器学习基石》第十一讲

配图均来自《台湾国立大学-机器学习基石》

---

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。